ESTIMASI TEGANGAN OPEN CIRCUIT DAN RESISTANSI INTERNAL BATERAI MENGGUNAKAN ALGORITMA RECURSIVE LEAST SQUARES

Paris Ali Topan; Dinda Fardila

doi:10.51401/jinteks.v6i4.4863

Authors

Paris Ali Topan Universitas Teknologi Sumbawa
Dinda Fardila Universitas Teknologi Sumbawa

DOI:

https://doi.org/10.51401/jinteks.v6i4.4863

Keywords:

Recursive Least Squares, Open Circuit Voltage, Internal Resistance, Battery Management System

Abstract

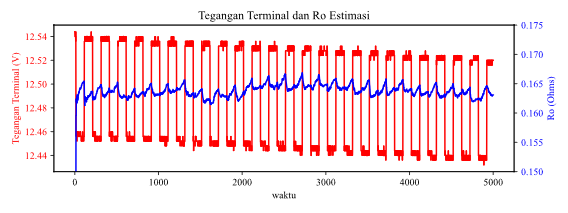
This study employs the Recursive Least Squares (RLS) algorithm to estimate the Open Circuit Voltage (OCV) and internal resistance (Ro) of a battery in real-time, based on measured current and voltage data. The results demonstrate that RLS can produce accurate estimates of OCV and Ro, with a Mean Squared Error (MSE) of 0.031, indicating a very small difference between the predicted and measured terminal voltage. The estimated OCV is stable, while Ro remains consistently within the range of 0.075 to 0.175 ohms, despite fluctuations in voltage due to changes in current. These findings show that the RLS algorithm can be effectively applied in battery management systems to dynamically and in real-time estimate parameters, which is crucial for applications such as electric vehicle battery monitoring and energy storage systems.

References

L. Zhou et al., “State Estimation Models of Lithium-Ion Batteries for Battery Management System: Status, Challenges, and Future Trends,” Batter. 2023, Vol. 9, Page 131, vol. 9, no. 2, p. 131, Feb. 2023.

P. Pillai, S. Sundaresan, K. R. Pattipati, and B. Balasingam, “Optimizing Current Profiles for Efficient Online Estimation of Battery Equivalent Circuit Model Parameters Based on Cramer–Rao Lower Bound,” Energies 2022, Vol. 15, Page 8441, vol. 15, no. 22, p. 8441, Nov. 2022.

P. K. Roy et al., “A Critical Review on Battery Aging and State Estimation Technologies of Lithium-Ion Batteries: Prospects and Issues,” Electron. 2023, Vol. 12, Page 4105, vol. 12, no. 19, p. 4105, Sep. 2023.

S. Park et al., “Review of state-of-the-art battery state estimation technologies for battery management systems of stationary energy storage systems,” J. Power Electron., vol. 20, no. 6, pp. 1526–1540, Nov. 2020.

K. Liu et al., “Towards Long Lifetime Battery: AI-Based Manufacturing and Management,” IEEE/CAA J. Autom. Sin. 2022, Vol. 9, Issue 7, Pages 1139-1165, vol. 9, no. 7, pp. 1139–1165, Jul. 2022.

F.?; Ghani, K.?; An, D. A. Lee, F. Ghani, K. An, and D. Lee, “A Review on Design Parameters for the Full-Cell Lithium-Ion Batteries,” Batter. 2024, Vol. 10, Page 340, vol. 10, no. 10, p. 340, Sep. 2024.

P. Venet, “Battery Performance, Ageing, Reliability and Safety,” Batter. 2023, Vol. 9, Page 277, vol. 9, no. 5, p. 277, May 2023.

M. F. Sgroi, “Lithium-Ion Batteries Aging Mechanisms,” Batteries, vol. 8, no. 11, Nov. 2022.

S. Wang, E. Zhang, H. Li, K. Jiang, and K. Wang, “Robust online parameter identification for batteries using exponential resetting recursive least squares,” Energy Proc., vol. 44, 2024.

S. Hoyer and J. Hamman, “xarray: N-D labeled Arrays and Datasets in Python,” J. Open Res. Softw., vol. 5, no. 1, p. 10, Apr. 2017.

R. Johansson, “Numerical python: Scientific computing and data science applications with numpy, SciPy and matplotlib, Second edition,” Numer. Python Sci. Comput. Data Sci. Appl. with Numpy, SciPy Matplotlib, Second Ed., pp. 1–700, Jan. 2018.

A. Marowka, “Python accelerators for high-performance computing,” J. Supercomput., vol. 74, no. 4, pp. 1449–1460, Apr. 2018.

G. Barletta, P. DiPrima, and D. Papurello, “Thévenin’s Battery Model Parameter Estimation Based on Simulink,” Energies 2022, Vol. 15, Page 6207, vol. 15, no. 17, p. 6207, Aug. 2022.

J. Benesty and T. Gänsler, “New Insights into the RLS Algorithm,” EURASIP J. Appl. Signal Processing, vol. 2004, no. 3, pp. 331–339, Mar. 2004.

M. El Marghichi, A. Loulijat, and I. El Hantati, “Variable recursive least square algorithm for online battery equivalent circuit model parameters identification for electric vehicles,” Electr. Eng., vol. 106, no. 3, pp. 2425–2445, Jun. 2024.

X. Du et al., “Online Identification of Lithium-ion Battery Model Parameters with Initial Value Uncertainty and Measurement Noise,” Chinese J. Mech. Eng. (English Ed., vol. 36, no. 1, pp. 1–10, Dec. 2023.

R. Havangi, “Adaptive robust unscented Kalman filter with recursive least square for state of charge estimation of batteries,” Electr. Eng., vol. 104, no. 2, pp. 1001–1017, Apr. 2022.

B. Ren, C. Xie, X. Sun, Q. Zhang, and D. Yan, “Parameter identification of a lithium-ion battery based on the improved recursive least square algorithm,” IET Power Electron., vol. 13, no. 12, pp. 2523–2530, Sep. 2020.

T. Zhu, S. Wang, Y. Fan, H. Zhou, Y. Zhou, and C. Fernandez, “Improved forgetting factor recursive least square and adaptive square root unscented Kalman filtering methods for online model parameter identification and joint estimation of state of charge and state of energy of lithium-ion batteries,” Ionics (Kiel)., vol. 29, no. 12, pp. 5295–5314, Dec. 2023.

V. Myilsamy, S. Sengan, R. Alroobaea, and M. Alsafyani, “State-of-Health Prediction for Li-ion Batteries for Efficient Battery Management System Using Hybrid Machine Learning Model,” J. Electr. Eng. Technol., vol. 19, no. 1, pp. 585–600, Jan. 2024.